Product Excellence Through Modern PLM in Fast-Paced Markets
Modern PLM systems empower businesses to achieve product excellence in fast-paced markets by enhancing collaboration, agility and innovation.
When navigating through the world of Machine Learning, Artificial Intelligence or Data Science (you name it), it is usually not long before coming across the term “Neural Network” or “Deep Learning”. They seem like the panacea for all tasks involving artificial intelligence, driving areas like computer vision, natural language processing, voice recognition and many more. However, for people that are not specialized in this field, neural networks or deep learning tend to seem like an obscure superpower solving very complex tasks.
To level the field of neural networks to all kinds of practitioners, we will publish a comprehensive series of blog posts dedicated to this topic in the coming weeks.
With our blog series, we want to make the neural network and its extensions more accessible. We will show that the fundamental principles of neural networks are based on simple mathematical computations that can be understood by anyone who has basic linear algebra or calculus knowledge. Understanding the basics will facilitate understanding the more complex use cases later in the series.
In our first blog today, we want to kick off with a journey into the history of neural networks. In the weeks following, we will lay out the basics of neural networks on a high level, starting with the simpler ideas, followed by more advanced extensions to these simple ideas. Overall, we hope the series will give you a better overview over this omnipresent topic in the Age of Data.
In this piece, we would like to look at how the idea of neural networks emerged, and what led the thinkers of early artificial intelligence towards that concept. The achievement of recreating some fundamental brain functionality by the method of neural networks has been fueled by a collection of ideas from areas such as philosophy, mathematics, economics, neuroscience, psychology, control theory, computer engineering, and to some extent, linguistics. First, it must be understood that the history of the so-called neural network can only be understood properly within the context of something larger: the strive towards intelligent systems. Alone finding a definition for intelligence can be quite boggling, especially since we naturally have sought to describe ourselves and how the inner core of our consciousness works since the Antique.
It is quite the journey through time, science and our brains, so buckle up as you embark on this story. The journey will take you from how brains make decisions and their cellular composition and interactions, all the way to what it means for a computer to mimic a brain. This article aims to tell the story of the inception of neural networks in simple terms. The goal is demystifying the neural networks concept and making it more approachable. First Station: Aristotle.
As philosophy is heavily involved with this intricate task, Aristotle is often cited as the initial starter of the idea that we can capture and formalize the parts of the brain that lead us to conclusions from a given set of rules. These so-called syllogisms are likely the first concept of a rule-based dataset as an input to a concluding entity.
All humans are mortal. – Proposition
All Greeks are humans. – Proposition
All Greeks are mortal. – Conclusion
Example for a syllogism as defined by Aristotle.
Once we know that, we can imply that algorithms running on machines could do the same – what is an algorithm but a set of instructions in a specific order? That’s a perfect principle for drawing conclusions based on rules as an input. Fast forward a couple of centuries, the contributions of Thomas Hobbes and René Descartes led to the formalization of thought: reasoning, causation and rationality became a part of calculus and computation – and when David Hume stepped into the game by introducing the linkage between knowledge and repeated exposure, the foundation for expressing intelligence by a machine had been set.
As much as a recipe is a key for baking a cake successfully, understanding how our brains function to generate thoughts is key for simulating it on a piece of inanimate circuits in a computer.
The tissue of our brains is made up of a neural mesh: Our nervous system consists of hundreds of billions of nerve cells that are interconnected via so-called synapses that serve as contact points between cells. This structure of the brain was first by proposed by Santiago Ramón y Cajal at the end of the 19th century. When experimenting with tissue samples, Cajal found that, when dipped in a silver nitrate solution, one can observe a reaction that turns the obscure into something more obvious: Lines begin to manifest that color the nerve cells and the complex network of connections between them. Later in 1906, Cajal was awarded the Nobel Prize in Physiology or Medicine (the original category caters to both disciplines) for this work “on the structure of the nervous system” together with Camillo Colgi, who invented the coloration technique.
This leap in understanding the workings of the brain was fundamental: It was already understood that one can transmit meaning over distances via electric signals, for example by switching on and off an electric current. Furthermore, the discovery that electric currents pulsating through nerves are also responsible for communication in organic lifeforms had already been made. Cajal’s and Colgi’s discovery that the brain matter consists of specific interconnected neurons led to the conclusion that they also communicate the same way: by means of electric signal transmission and processing.
A neuron consists of its body (soma) and strands that look like a frayed-out extension of that cell body. We can distinguish between two types of these strands: Dendrites, of which the neuron has multiple, and one single axon per cell. The dendrites are responsible for receiving signals from other neurons, while the axon (through its terminal buttons) takes care of sending an output signal to the neurons it connects to. Together with the synaptic cleft that separates transmitter and receiver cells, the dendrites of the receiver cell and the terminal buttons of the transmitter cell form the synapse.
When viewed as a whole, this complex network of receiving input signals via dendrites and producing one output signal via the axon is how information via electric impulses traverses the brain. There is a certain mechanic to why and how neurons form these connections, not every neuron is linked to every other neuron. When we observe the so-called “gray matter” in brain imagery, essentially what we describe are the cell bodies of the neurons. What follows next, as we talk about how that idea can be applied in a non-organic, emulated context on a computer, we must keep in mind that the neural networks we use in computation are a gross simplification of what happens in our brains, albeit a beautiful one.
Anyhow, researchers always had a profound interest in copying, imitating, and therefore claiming understanding of our brains and ourselves. An important step towards a field yet to be determined as Artificial Intelligence was made by McCulloch and Pitts, who created what can be understood as the first artificial neuron in the early 1940s: the threshold logic unit (TLU). It was designed specifically to model the mesh of neurons we have in our brains. We have already learned that neurons perceive electric input signals from the ones that connect to their dendrites. What happens (next) inside the neuron is some sort of activation: Neurons do not fire all the time, and they do not always send a signal to their neighboring neurons via their axons. This sort of activation – when a neuron fires versus when it does not – highly depends on the input. One rule of thumb became famous in that regard: “Neurons that fire together, wire together”. The degree of activation (“firing”) or conversely the degree of inhibition (“not firing”) is related to the input that neurons receive from other neurons that connect to it. That notion strongly resembles what happens in a circuit: on or off, zero or one, energy flowing or not.
If we interpret the communication between neurons in such a manner, we can think about implementing simple logic already: A neuron that fires means “true”, a neuron that rests means “false”. If we want to conceptualize this idea some more, how do we reach logical “true” and “false” with multiple inputs though? In simpler terms, how do we get to “firing” or “not firing” when a neuron receives signals from a handful of previous neurons, and from others they just get silence?
The researchers converted the neurons they modeled as inhibitors of a threshold function. What that means is that each neuron must contain a threshold value to fire: Say this threshold is 1, then in order to make the neuron fire, the sum of its inputs must reach 1. Otherwise, it shall remain silent. By combining and defining thresholds as well as signal strengths, we can model logic.
For example, say we have a threshold of 2 and two inputs that have a value of 1: In this case the two inputs summed together reach the threshold and the neuron shall fire. That corresponds to the logic AND. If we were to define the threshold as 1 and kept the inputs the same, we’d have an OR, because any of the inputs from previous neurons is enough to trigger the activation. In a nutshell: Any neuron receives an input signal from the previous neurons it is connected to. These inputs are added together, and the produced sum goes through an activation function as its argument. By that, we can simulate similar logic to electric circuits, because the way electrical signals are propagated in circuits is somewhat similar to how our nerve cells’ synapses work – on a very abstract level.
Remember the heuristic that neurons that fire together also wire together? The more often neurons fire together, the stronger their connection becomes. We simulate this connection by modifying the output of a certain neuron with a weight, depending on the downstream neuron it communicates with – and how often they have communicated in the past. Logically, the more communication has taken place, the higher the weight. This gives us a schematic for an artificial neuron:
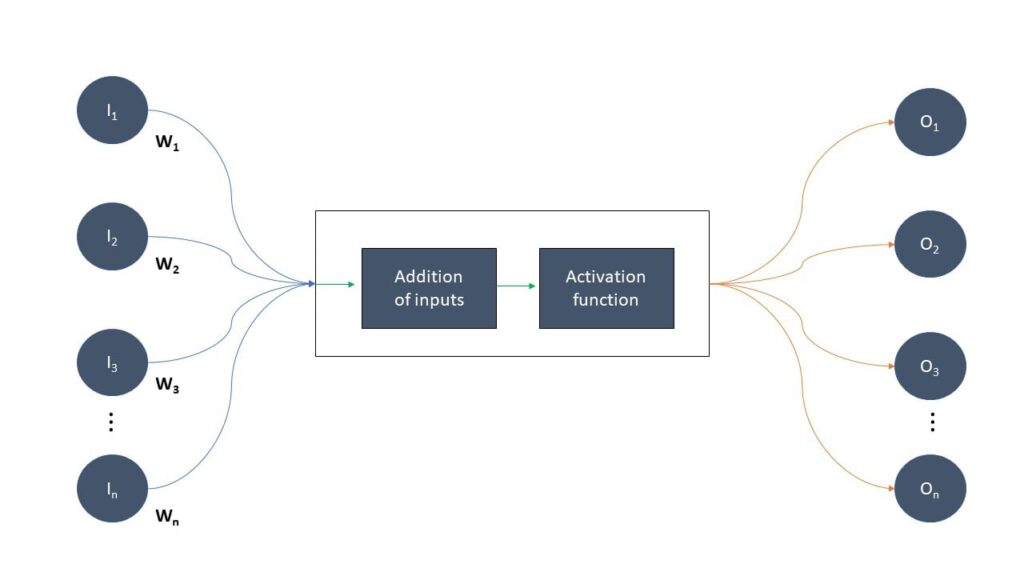
This emulation of a neuron is particularly suitable for a very popular question in the domain of machine learning and artificial intelligence: Does an input belong to a certain class? For example, speaking in simple terms: Does an image contain a certain shape or color? This is because we can take a set of inputs, say even vectors, and present their summation (or dot product for vectors) to a simple, binary, yes-no based activation function. The concept of the perceptron grew out of this idea, introduced by Frank Rosenblatt in the late 1950s. The Rosenblatt perceptron starts with the values for the weights and the activation function, and then confronts that artificial neuron with the so-called training set. That means we show it a series of data where we know something about the information we want to predict.
Say we want to have our neuron later infer, or guess, whether it has seen an image of a triangle or not. Hence, we will repeatedly calculate the output for each example of an image that contains shapes. We can do so by decomposing every image into its pixel’s color or saturation values. Those pixel values are fed as inputs to our network, and their weighted sum determines if the activation function fires or not, or equivalent, if the image contains a triangle or not.
But what if our function got the output wrong? Exemplified based on our example, in simple terms the learning rule for a neural network goes as follows: Take every image and calculate its output. If the output calculated is wrong, the weights attached to the inputs get adjusted. Otherwise, if the output is correct, the weights stay unchanged. If the true output is 1 (contains triangle), but the predicted output is 0 (no triangle), the weights would need to be increased in order to have a higher chance of exceeding the threshold that makes the activation function fire. In the exact opposite scenario, the weights would need to be decreased so that the activation does not fire. This process is continued until the prediction output is satisfactory (e.g., 95 percent of images classified correctly) or we reach a point where we can’t improve the results even after repeated adjustments of the weight parameters.
The concept just described is called Single-Layer Perceptron and manifests the simplest version of a neural network. There are a lot of extensions and variants of them, but before jumping to those, we will take a deeper look at the Single-Layer Perceptron in our next part, accompanied by a Python notebook for illustration. Stay tuned!
We thank Tobias Walter for his valuable contribution to this article.
Modern PLM systems empower businesses to achieve product excellence in fast-paced markets by enhancing collaboration, agility and innovation.
Read how the Campaign Planner & Designer (CPD) helps you to manage supply chain variability.
Explore automated production planning with our Campaign Planner & Designer.
The pharma market trends impact logistics with a shift to smaller, higher-value shipments and new temperature requirements.
© Camelot Management Consultants, Part of Accenture
